
10年程前、私は四次元をテーマにしたマンガ詩集を描いていた。
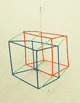
そのとても不思議な宇宙船の骨組みのようなモビールを、私は、ベルリンのフィンランド館のクリスマスバザーで初めて見かけた。

短編マンガ

私は電話中にもじゃもじゃした毛のような落書きを描くのですが、ある日描いた落書きは、なかなかの傑作でした。私はそこで、一筆書きの可能性を感じ、一筆書きを始めました。

ペンローズ・タイルとは、イギリスの物理学者ロジャー・ペンローズが考案した二種類の菱形のタイル模様です。正方形や六角形などのタイルと違い、ペンローズタイルは、並べていくと二度と同じパターンが現れないということが、証明されているそうです。このような単純な二種類の形の組み合わせが、無限に違った模様を作り出すということに感銘を受けました。世の中の仕組みもこのようなものかもしれません。このような複雑な世界を作り出している要素は、単純な仕組みの組み合わせなのではないでしょうか。

もう一年も前のものですが、中世イスラム芸術と『ペンローズ・タイル』について述べた記事があります。 イスラム建築のモスクや宮殿に装飾されている「ギリー」と呼ばれる複雑なパターンは、長い間、直定規とコンパスで作られたと思われていたが、最近(2007年)になって、ギリーの一部は、幾何学的タイルを組み合わせて生み出されたものだと判明したそうです。

私はドーナツ型にとても興味を持っています。 有名な話ですが、ドラクエなど多くのRPGゲームの世界は球体ではなく、ドーナツ型だそうです。北端を越えると、南端から出てくる。東端を越えると西端から出てくる。

赤、白、青、緑、それぞれの蛇は、同じ形の絡まり方をしています。最初に赤い蛇を描き、90度ずつずらして他の色の蛇を描きました。

これは、何の展開図でしょうか? どう見ても、立方体になりそうです。

まぶたを閉じて、じっくり、まぶたの裏に映し出される映像を堪能したことはありますか。複雑な幾何学がつくりだすイメージは万華鏡を見ているような、不思議な気分になりませんか。 そのようなイメージは、脳の知覚のしくみ自体から発生しているのではないか。もともと知覚中枢の構造に内在するイメージなのではないか。そして、そのイメージは時として、科学の重大な発見の大きなヒントとなっているのではないか。

花札と言えば、美しい図案が特徴です。すすきの山などは、あまりのシンプルな美しさに、ホレボレしてしまう方も多いと思います。しかし、今や、21世紀。花札を3次元化してみました。ふだん見慣れたものが、立体化されると、ひどく違ってみえませんか。

牛耕式とは、写本や銘文の書記に用いられた古代の筆記方式で、右から左に書いた次の行は左から右、その次の行は右から左というように、左右交互に進む書式のことです。
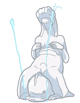
何年か前に、ローマで蚊が大量発生したそうである。調べてみると、古代ローマ時代から現代まで使われている下水道が原因だと判明。ローマに住んでいる人々は気づいた。「そういや、下水道が作られてから2000年もの間、誰も掃除してなかったな・・」

これは、4次元世界から見た私の肖像です。 私は、四次元の世界の描き方を研究しています。Rudy Ruckerの「四次元の冒険」というすばらしい本を紹介します。 この本は、二次元と三次元の違いを例にしながら、四次元の世界を理解するトレーニング方法が書いてあります。

一般的な地図は鳥瞰図ということで上から見た地図になっていますが、中国のある民族は地下から見上げて書く土竜図を使っていたそうです。(でも私たちも、星座の図は、下から見た図です)
